冒泡,选择,插入,归并,堆排,快排,基数
排序算法

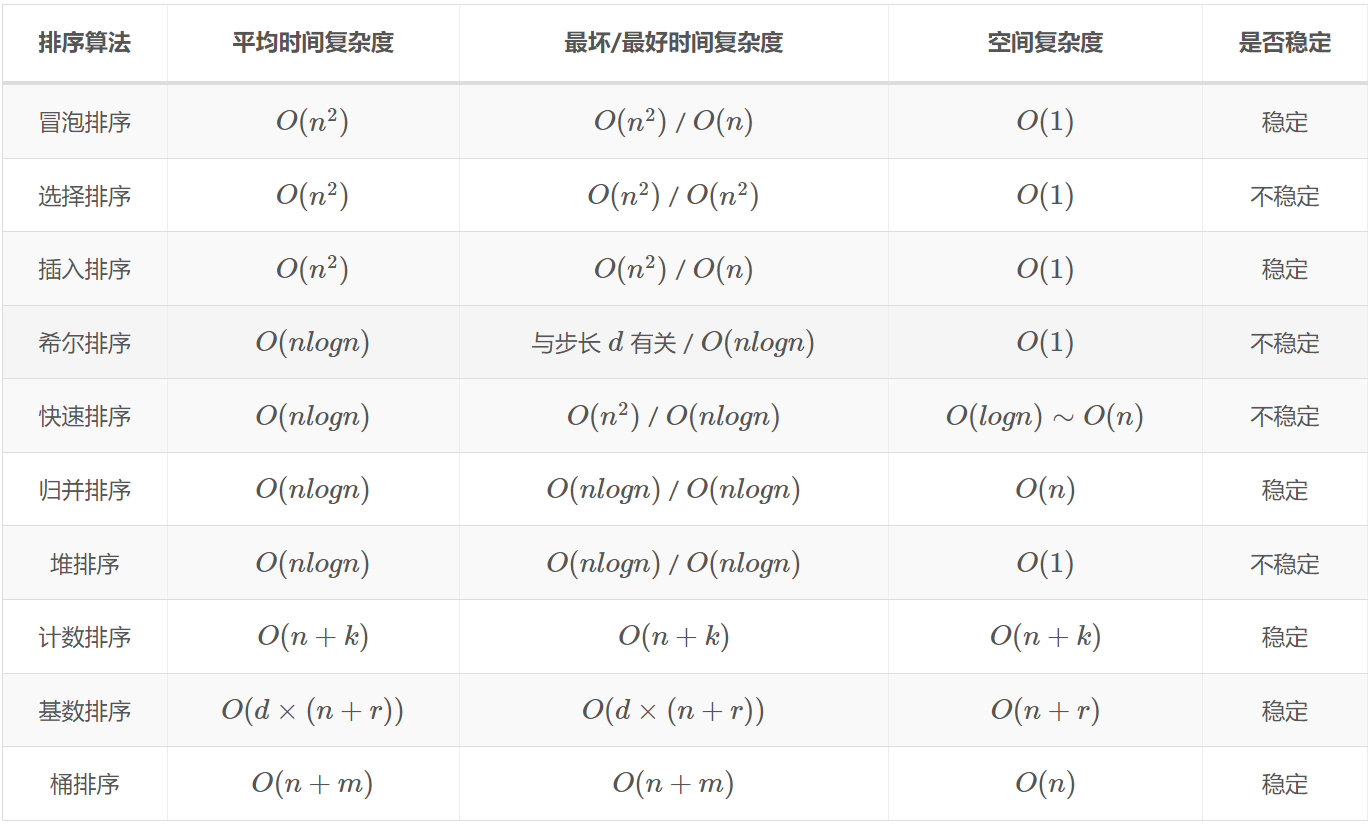
- 比较排序算法: 冒泡, 选择, 插入, 归并, 堆排, 快排
- 非比较排序算法: 计数, 基数, 桶排
- 稳定性: 7 个常用算法, 3 稳(冒泡, 插入, 归并) 4 不稳 (选择, 希尔, 快排, 堆排)
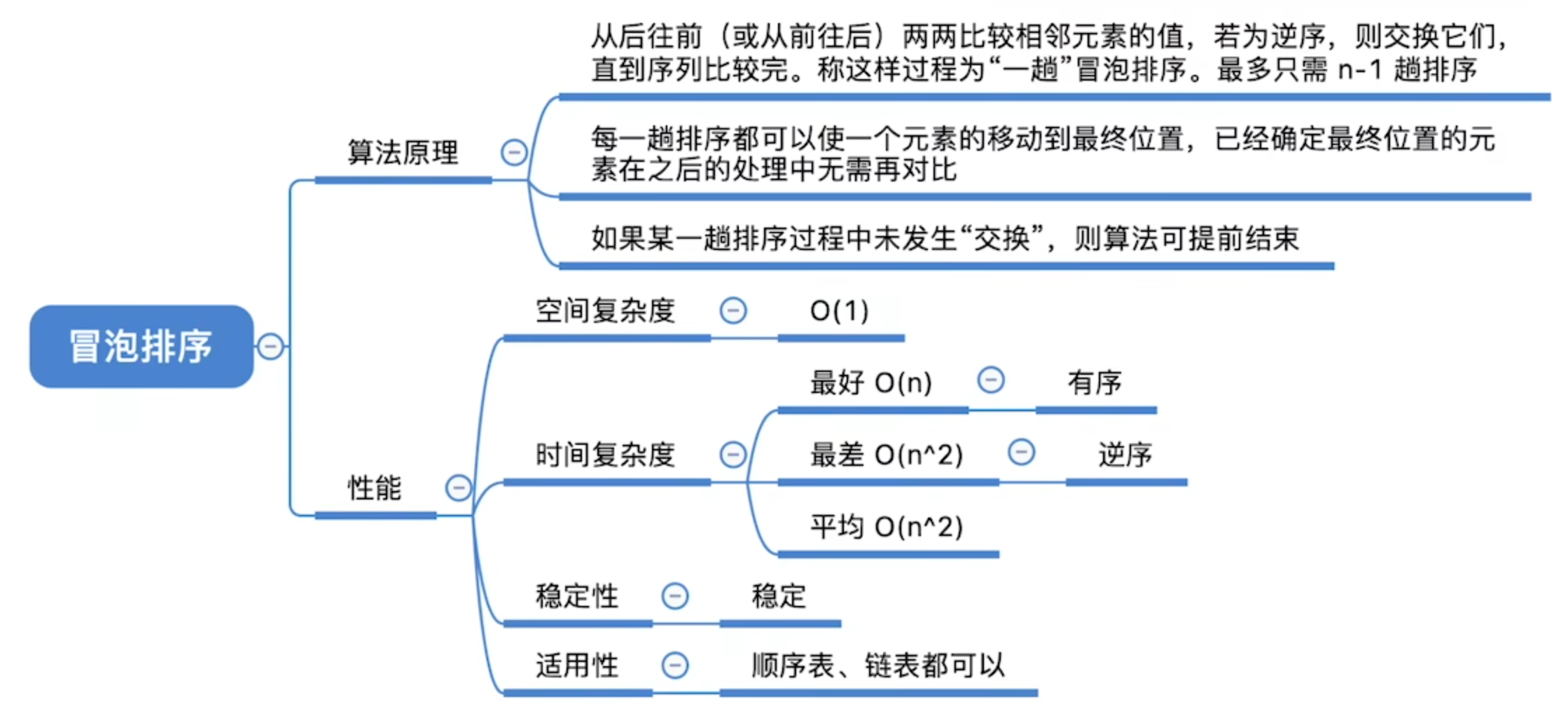
冒泡排序
从后往前, 相邻的数据两两比较, 一趟完成后, 第一个元素为最大/小值
C++实现:
void bubble_sort(vector<int> &input){
for(int i=0; i<input.size(); i++){
for(int bubble = input.size()-1; bubble>i; bubble--){
if(input[bubble-1] < input[bubble] ){ //为了保证排序的稳定性, 这里不要用 <=
int temp = input[bubble];
input[bubble] = input[bubble-1];
input[bubble-1] = temp;
}
}
}
}
(改进)冒泡排序: 鸡尾酒排序
冒泡排序是只在一个方向上进行排序, 鸡尾酒排序是从前往后和从后往前交替排序(即先找最大, 再找最小). 在面对大部分元素已经有序的数组时, 鸡尾酒排序的时间复杂度接近于 O(n).
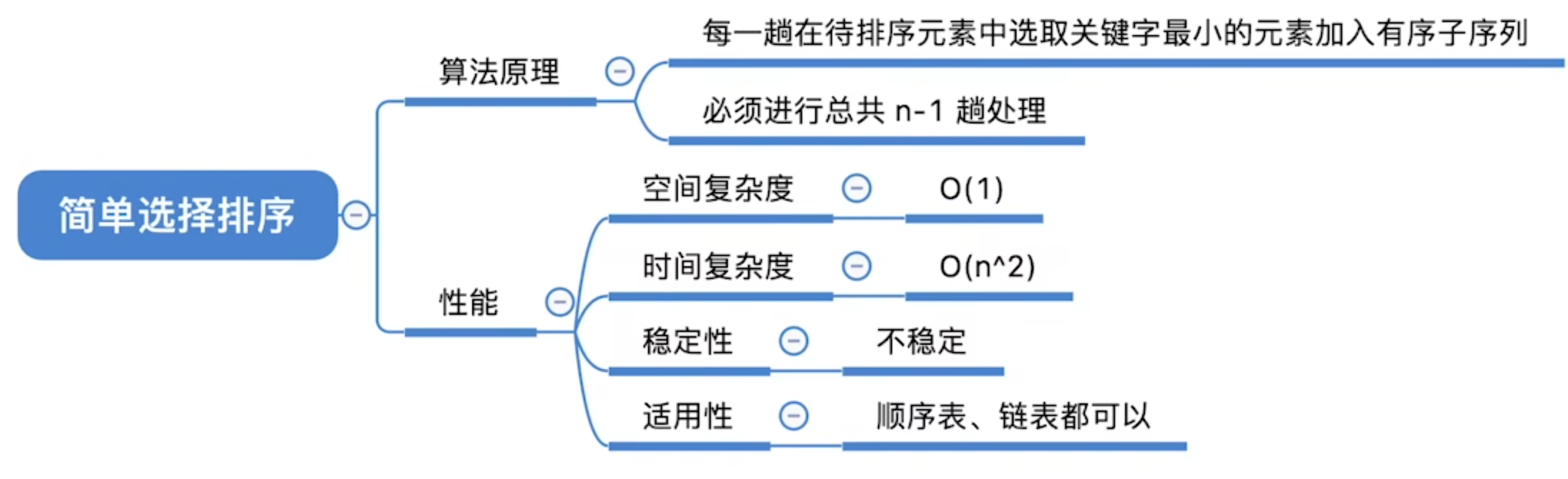
选择(交换)排序
在未排序序列中找到最小(大)元素, 存放到起始位置;然后再从剩余的序列中继续寻找最小(大)元素, 并将其放到起始位置的下一个位置;以此类推, 直到所有元素排序完毕.
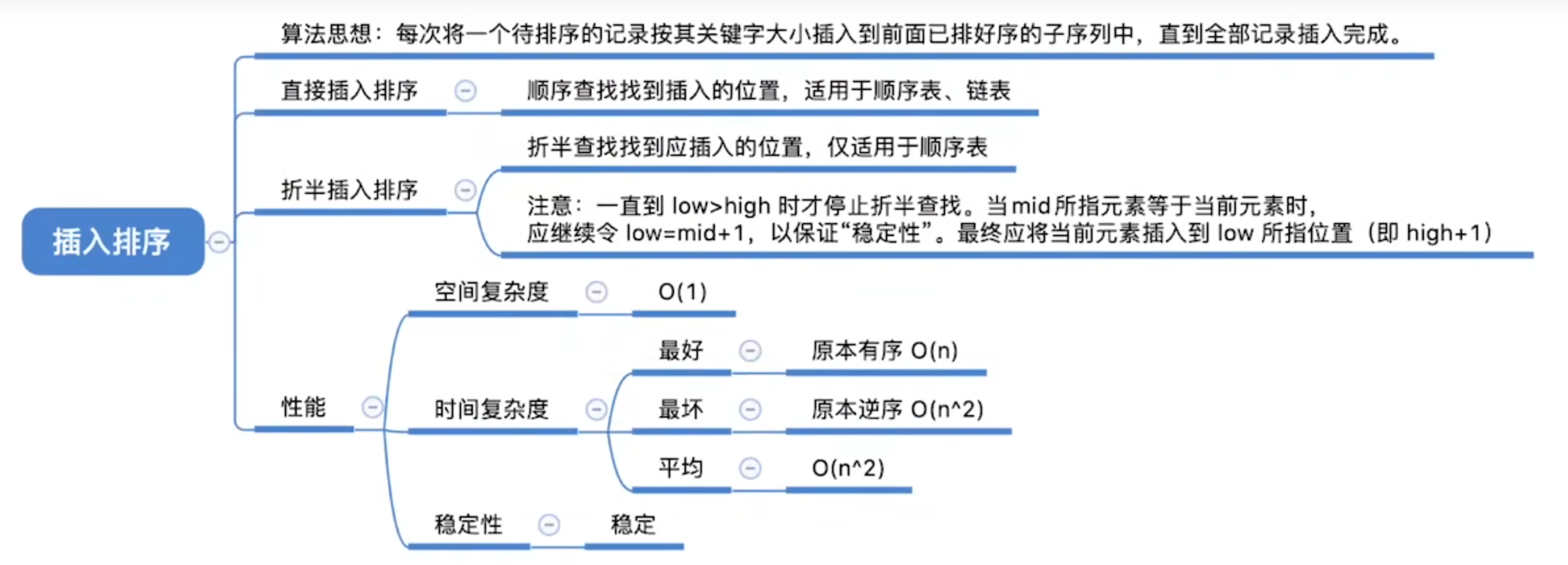
插入排序
-
从第一个元素开始,该元素可以认为已经被排序
-
取出下一个元素,在已经排序的元素序列中从后向前扫描
-
如果被扫描的元素(已排序)大于新元素,将该元素后移一位
-
重复步骤3,直到找到已排序的元素刚好新元素的位置
-
将新元素插入到该位置后
-
重复步骤2~5
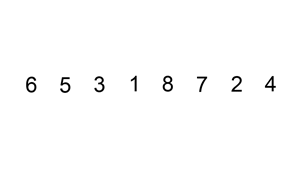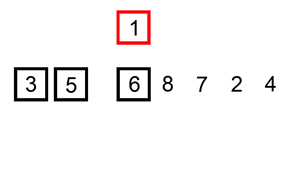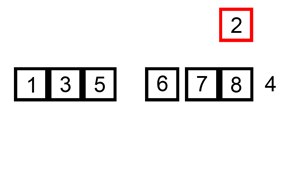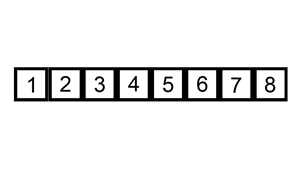
(改进)插入排序:二分插入排序:
直接插入在查找插入位置时, 可以采用二分查找的方式(因为已经有序), 这样可以减少查找插入位置时花费的时间.
希尔排序

希尔排序(Shell Sort), 也叫递减增量排序, 其实质是分组插入排序, 是插入排序中一种更高效的改进版本. 插入排序具有以下两点性质:
-
对于几乎已经排好序的数据操作时, 效率很高, 可以达到线性排序的效率;
-
插入排序在每次往前插入时只能将数据移动一位, 这使得效率较低.
因此, 希尔排序的思想是:
-
首先选取一个合适的步长(gap < n)作为间隔, 并将所有元素划分成 gap 个子序列, 每个子序列 内部元素之间的距离都是 gap.
-
分别对每个子序列使用直接插入排序.
-
缩小步长 gap 的值, 重复上面的分组和插入排序过程, 直到 gap = 1 为止.
快速排序
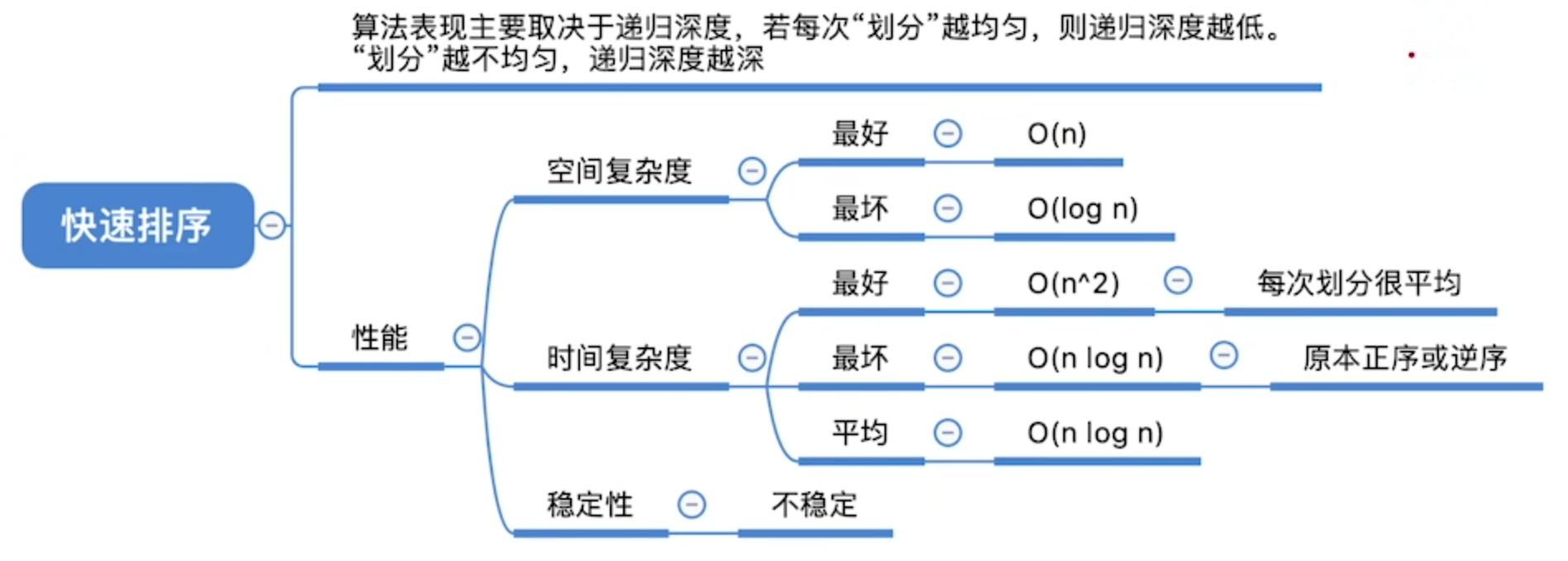
C++递归实现:
void quickSort(vector<int>& input, int low, int high){
if(input.size()==0 || low<0 || low>=input.size() || high<0 || high>=input.size()){
cout<<"error";
exit(0);
}
int mid = Partition(input, low, high);
if(mid<high) quickSort(input, mid+1, high);
if(mid>low) quickSort(input, low, mid-1);
}
int Partition(vector<int>& input, int low, int high){
int p = input[low];
while(low<high){
// 一定要high在前, 否则会造成数组元素覆盖
while(low<high && p<=input[high]) high--; //这里注意, 如果忘了写=号, 就会陷入死循环
input[low] = input[high];
while(low<high && p>=input[low]) low++;
input[high] = input[low];
}
input[low] = p;
return low;
}
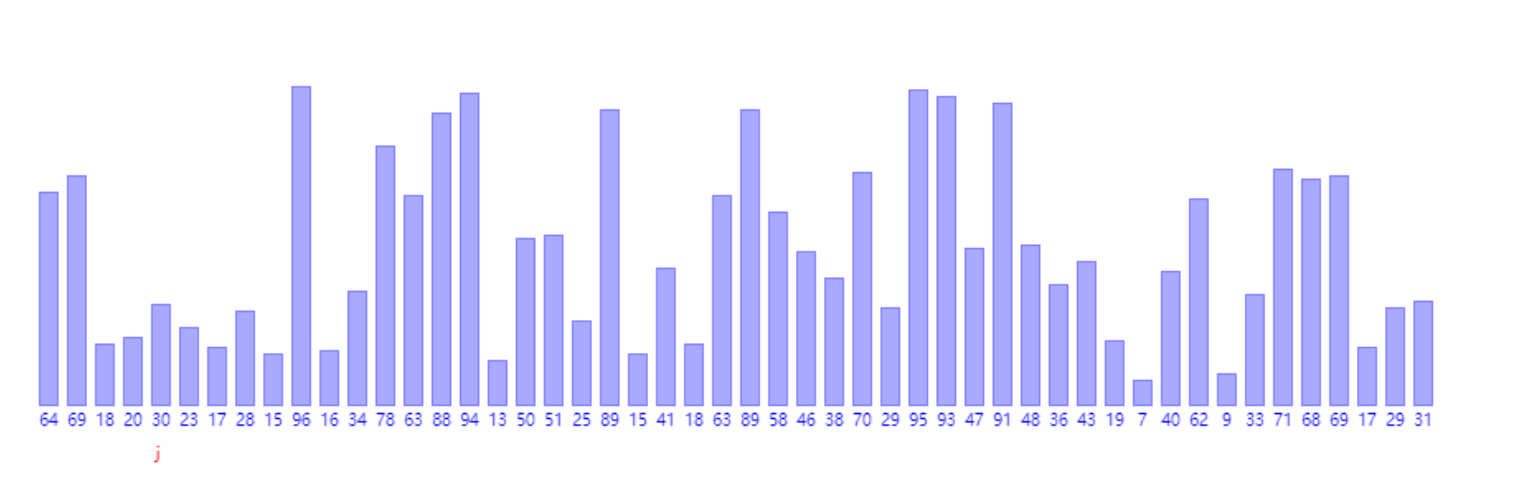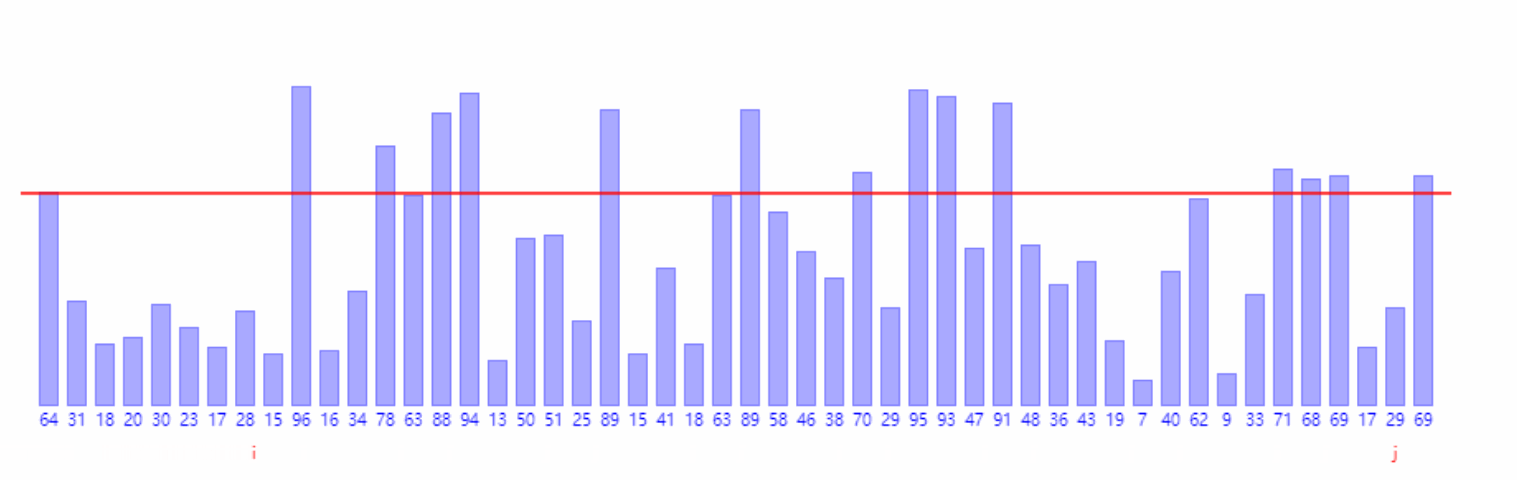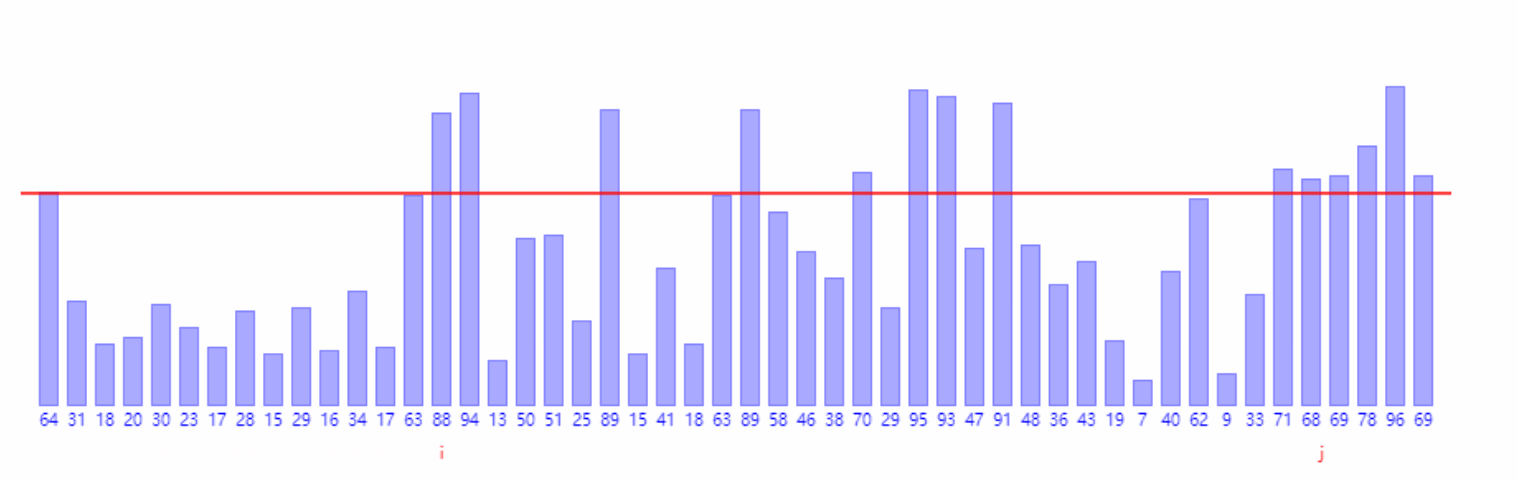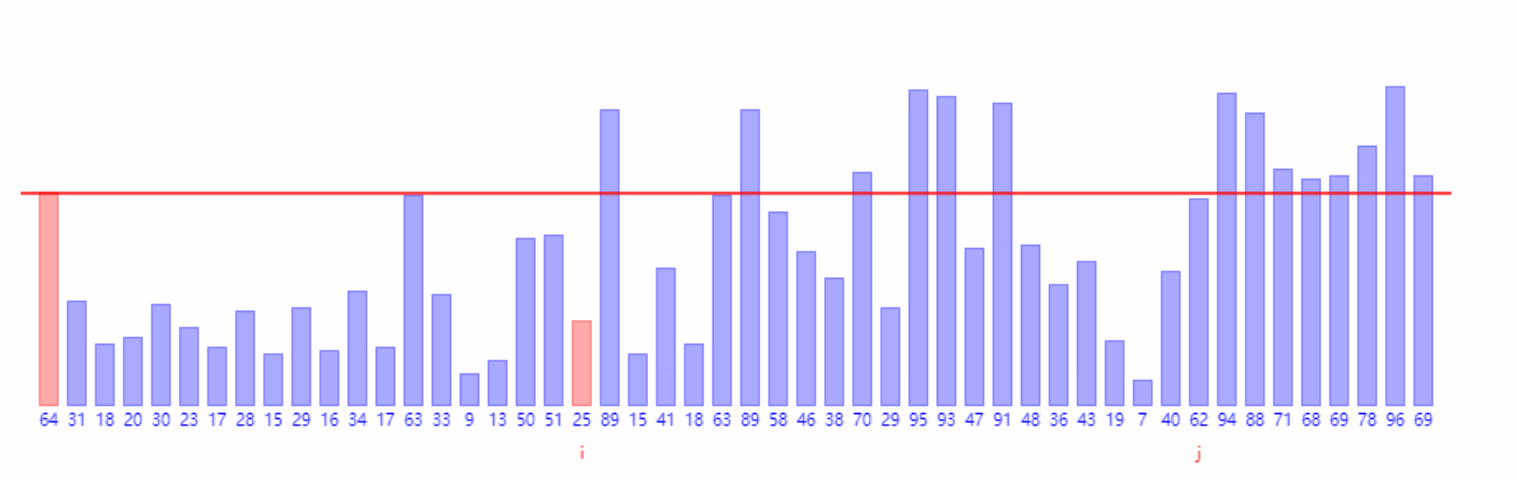
归并排序
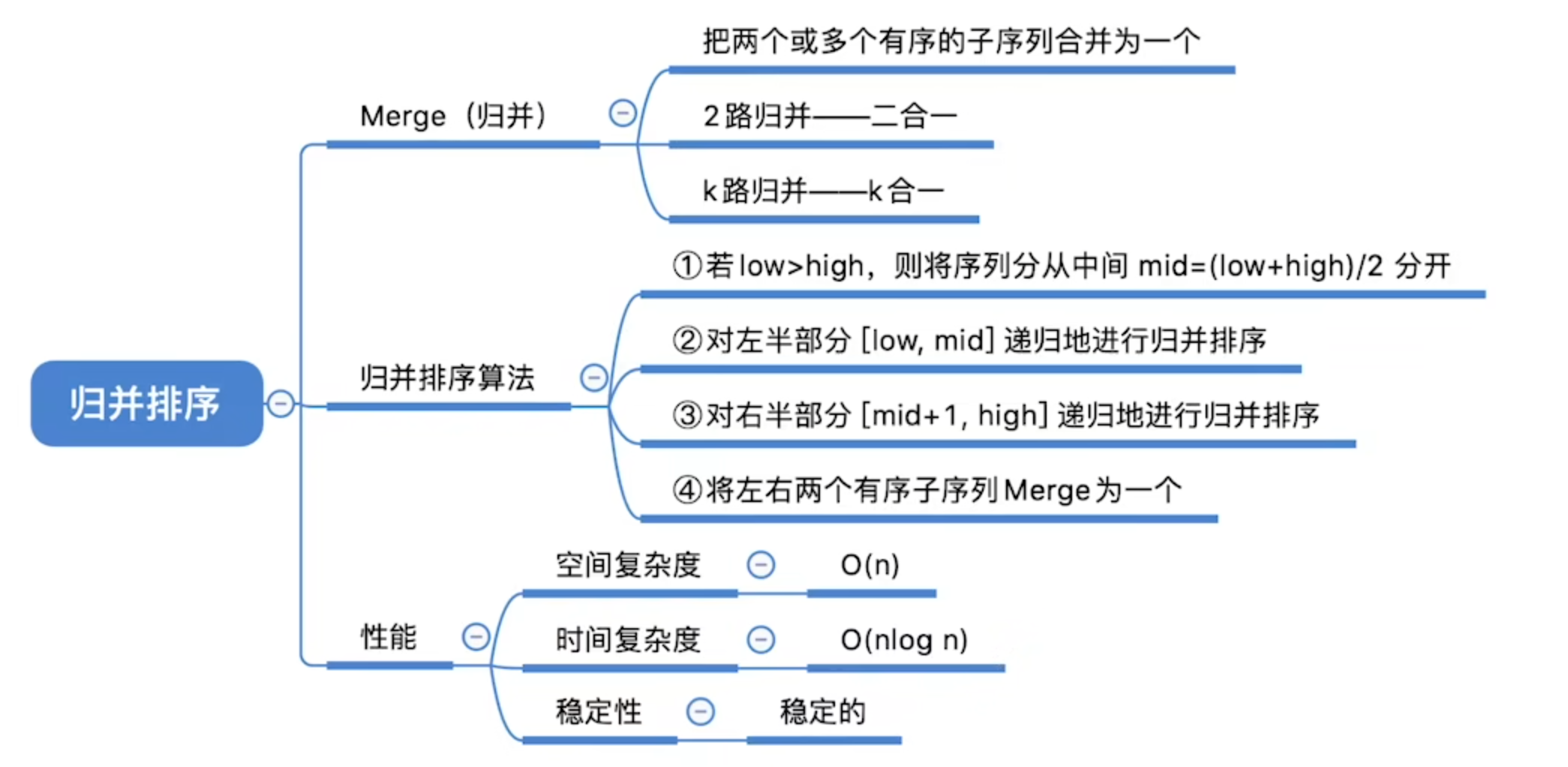
C++递归实现:
void mergesort(vector<int>& a,int first, int last){
if(first<last){
mid = (last+first)/2;
mergesort(a, first, mid);
mergesort(a, mid+1, last);
mergeArray(a, first,mid,mid+1,last);
}
}
void mergeArray(vector<int>& a, int first1,int last1,int first2,int last2){
vector<int> temp;
int i = first1;
int j = first2;
while(i<=last1 && j<=last2){
if(a.at(i) < a.at(j)){
temp.push_back(a.at(i));
i++;
}
else{
temp.push_back(a.at(j));
j++;
}
}
while(i<=last1){
temp.push_back(a.at(i));
i++;
}
while(j<=last2){
temp.push_back(a.at(j));
j++;
}
for(int i = 0; i<temp.size(); i++)
a.at(first1+i) = temp.at(i);
}
堆排序
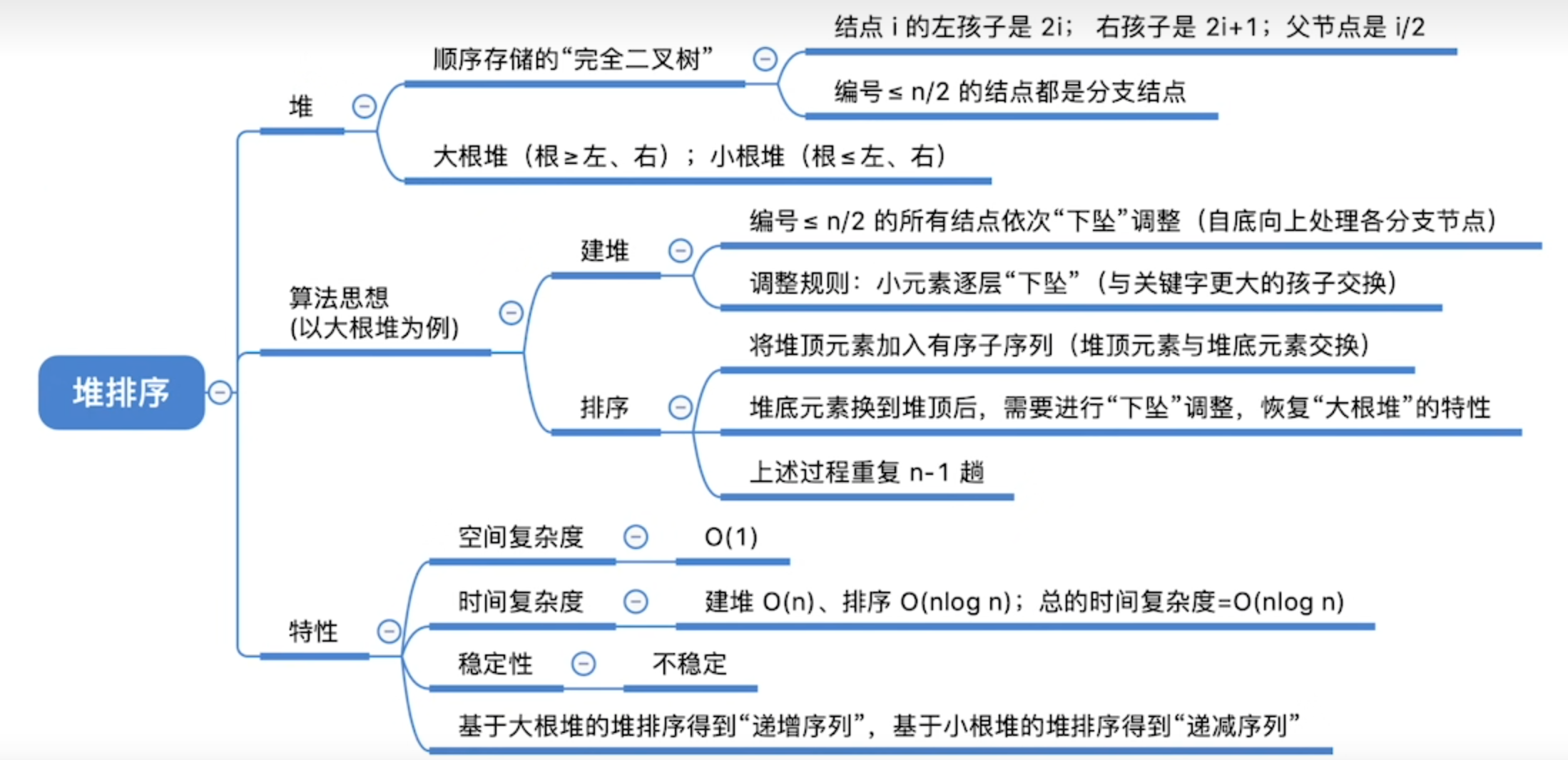
基数排序
